Unless stated otherwise, seminars take place at LMF, ENS Paris-Saclay, 4 avenue des Sciences, 91190 Gif-sur-Yvette, France. Most talks should have a link attached to attend online, if none is present please contact Théo Winterhalter, and we'll see what we can do. To stay informed, you can subscribe to our mailing list.
Access the list of seminars from before 2024.TBA
On 22 January 2026, at 14:10, in room 1Z28.
Ciarán Dunne (Telecom Paris Sud)
Attend onlineTBA
Indexing and Retrieval in a Heterogeneous Formal Library
Was on 8 January 2026.
Abdelghani Alidra (Deducteam)
Dedukti and MMT are both examples of tools that can collect mathematical libraries coming from different systems in a unified but heterogeneous body. Indeed, both tools implement a logical framework where the logics or type systems of the various mathematical assistants can be represented, so that their libraries can be encoded in a single format preserving well-typedness. Still, the images of the various libraries remain disjoint: logical consistency of their union is not granted, the encoding of the various statements differs from logic to logic, and the same mathematical entity remains defined repeatedly and independently. To benefit from the common representation, then, additional tools need to be developed, for example, to translate results encoded in the representation of a logic into the representation of a stronger logic, taking care of aligning the duplicated mathematical entities.
In this talk we present the challenges posed by indexing and searching the large, heterogeneous library. For example, users may expect to find results in the library up to the encoding used and up to alignments, so to be able to mix in the search result statements originally coming from different systems and logics. In particular, we describe new indexing and retrieval capabilities that we integrated directly into the LambdaPi proof assistant, that can work on Dedukti files.
Two-Variable Logic for Hierarchically Partitioned and Ordered Data
Was on 27 November 2025.
Vincent Michielini (Université de Bordeaux)
It is known that the satisfiability and finite satisfiability problems for Two-Variable First-Order Logic (FO²) remain decidable when the logic is extended with one or two equivalence relations, but become undecidable with three. In this talk, we investigate the fragment of FO² enriched with a nested sequence of equivalence relations E1 ⊆ E2 ⊆ E3..., which can represent data partitions of increasing granularity (for example, E1 may relate people living in the same building, E2 those living on the same street, and so on).
We show that, despite the presence of arbitrarily many nested equivalence relations, both satisfiability and finite satisfiability remain decidable, and we establish tight complexity bounds. We also present analogous results for several natural extensions of the framework—including the addition of a linear order or nested total pre-orders, along with a few motivating applications.
Unification for pattern matching in Agda Core
Was on 13 November 2025.
Ewen Broudin--Caradec (Deducteam)
Agda Core is a project of a formally verified core language in Agda. Due to some design choice and to keep the core syntax very close to Agda's syntax, a unification algorithm for pattern matching is included in this project. This seminar will explain why this algorithm is needed and discuss its specification.
Lean4Less: Translating Lean to Smaller Theories via an Extensional-to-Intensional Translation
Was on 6 November 2025.
Lean is a proof assistant developed by the Lean FRO that has become especially popular with mathematicians in recent years, whose type-theoretic foundations take after the proof assistant Rocq. While Lean's typechecking kernel attempts to be as minimal as possible, it introduces a number of specialized definitional equalities as conveniences for mathematical formalization. While crucial to enabling scalable formal developments in Lean, these definitional equalities complicate metatheoretical analyses and the task proof export from Lean.
In this talk, I will discuss the theory, design, and implementation of a tool called "Lean4Less" that translates Lean proofs to a smaller theory "Lean-" with fewer such definitional equalities, focusing in particular on the elimination of Lean's rules of proof irrelevance and "K-like reduction". Lean4Less implements a special case of a translation from extensional to intensional type theory, inserting explicit type conversions around subterms using generated type equality proofs that are typeable in the Lean- theory. Lean4Less's implementation is based on a modification of a typechecker kernel for Lean taken from the "Lean4Lean" project, and effects our translation by generating translated terms in parallel to normal typechecking.
An overview of Coqine
Was on 23 October 2025.
I'll give an overview of the architecture of Coqine, a translator from Coq/Rocq to Dedukti. I'll review the main features of the tool and discuss possible improvements related to the recent changes in the implementation of Rocq.
Why Docker isn’t enough: Building software environments that stay reproducible over time
Was on 22 October 2025.
Théo Zimmermann (Télécom Paris)
Complex software setups can be difficult to reproduce after some time. Tools like Docker make it easy to share software environments, but they don't guarantee that those environments can be rebuilt exactly in the future. By rebuilding thousands of existing Docker images and Nix software packages, we show that functional package management offers a stronger foundation for reproducibility, one that endures across time and machines.
Dependent programming in Rocq with proxy-based small inversions
Was on 16 October 2025.
The different techniques of inversion present in Rocq all have the same problem of creating large and difficult to read proof terms. While this is rarely a problem, dependent functions defined in a library with inversion are then not readable to a user trying to understand them. Small inversions were created to have an inversion method that creates lightweight proof terms that can be used for dependent programming. We present a version of small inversions, proxy-based small inversions, that rely on preemptively defining inductive types that mimic specialised instances of the type of the object we seek to invert.
PhD Defence: Aspects of Category Theory in Proof Assistants
Was on 7 July 2025.
Luc Chabassier (Deducteam)
Luc will defend his PhD thesis.
Aspects of Category Theory in Proof Assistants
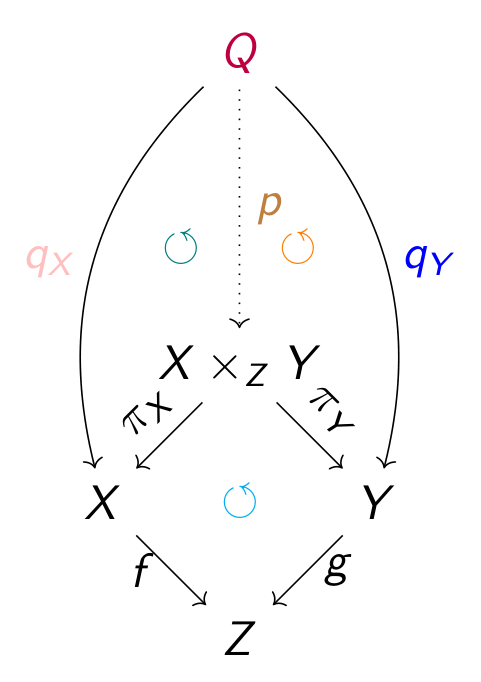
While the use of proof assistants in mathematical research has yet to become the norm, an increasing number of results have been formalized. The prevalence of category theory in recent mathematical research indicates the need for its formalization in proof assistants. However, category theory is challenging to formalize for reasons we will explore.
The first difficulty is due to the fact that proposition equality in dependently typed theories as a structure that interacts in a complicated way with categories formalised inside those theories. We describe those challenges, and propose some solutions we explored to this problem.
The second difficulty is more pragmatic. One big advantage of category theory is its ability to be reasoned with using graphical languages. However, most proof assistants are text based; thus their notation systems cannot express any graphical language. We implement a plugin to graphically progress category theory proofs in the Coq proof assistant. After a quick demo, we will describe the different challenges in the implementation of such a software.
The defence will be in English.
Jury:
- Assia MAHBOUBI, Inria, Referee and Jury Member,
- Damien POUS, CNRS, Referee and Jury Member,
- Ambroise LAFONT, École Polytechnique, Jury Member,
- Paul-André MELLIÈS, IRIF, Jury Member,
- Samuel MIMRAM, École Polytechnique, Jury Member,
- Clément PIT-CLAUDEL, École Polytechnique Fédérale de Lausanne, Jury Member.
- Gilles DOWEK, Inria, Supervisor,
- Bruno BARRAS, Inria, Assistant Supervisor.
Monad Translations for Higher-Order Logic
Was on 3 July 2025.
Thomas Traversié (Deducteam)
Classical logic can be embedded into intuitionistic logic by inserting double negations in formulas. Several translations generalize this idea by using monad operators instead of double negations. They eliminate particular axioms, for instance the principle of excluded middle or the principle of explosion, and therefore can be used to embed classical logic into intuitionistic logic or intuitionistic logic into minimal logic. Such translations have been defined for first-order logic.
In this paper, we define a translation, parameterized by monad operators, for higher-order logic. In particular, the property that any formula and its translation are equivalent in the presence of the eliminated axiom holds under functional extensionality and propositional extensionality. We apply this translation to embed higher-order classical (respectively intuitionistic) logic into higher-order intuitionistic (respectively minimal) logic. By adapting Friedman's trick, we identify fragments of higher-order logic for which we can actually constructivize the proofs without modifying the proven statements.
This talk was presented at FSCD 2025.
Canonicity in Cubical Type Theory
Was on 12 June 2025.
Nicolas Margulies (Deducteam)
--
Code Generation via Meta-programming in Dependently Typed Proof Assistants
Was on 22 May 2025.
Mathis Bouverot-Dupuis (ENS Paris)
Dependently typed proof assistants offer powerful meta-programming features, which users can take advantage of to implement proof automation or compile-time code generation. This paper surveys meta-programming frameworks in Rocq, Agda, and Lean, with seven implementations of a running example: deriving instances for the Functor type class. This example is fairly simple, but sufficiently realistic to highlight recurring difficulties with meta-programming: conceptual limitations of frameworks such as term representation -and in particular binder representation -, meta-language expressiveness, and verifiability as well as current limitations such as API completeness, learning curve, and prover state management, which could in principle be remedied. We conclude with insights regarding features an ideal meta-programming framework should provide.
Informath: Interlingual autoformalization and informalization with Dedukti and GF
Was on 10 April 2025.
The project Informath develops conversions between formal and informal languages of mathematics, at the moment targeting Dedukti, Agda, Coq, and Lean on the formal side and English, French, and Swedish on the informal side. The core of Informath is a two-way conversion between Dedukti and MathCore, an abstract syntax of natural language in GF (Grammatical Framework). Dedukti is used as an interlingua for the formal systems, whereas MathCore is an interlingua for natural languages. By extending the abstract syntax, Informath aims to cover larger fragments of actual mathematical language as found in articles and books.
PhD Defence: Combining computational theories
Was on 3 February 2025.
Emilie Grienenberger (LMF)
Emilie will defend her PhD thesis.
Combining computational theories
Proof checkers and proof assistants are used to formalize mathematical theorems and verify software, notably critical systems such as medical, industrial and transport systems. The diversity of proof systems raises the question of their interoperability: how can proofs be rechecked and reused across systems? Logical frameworks such as the λΠ-calculus modulo theory provide a common formalism in which various logical systems and mathematical theories can be expressed. The proof transformation tools within the λΠ-calculus modulo theory allow proofs to be translated from one logical system another. In a similar way to logical frameworks, theories combining several theories provide a common language between theories. The main focus of this manuscript is the study of the definition and properties of these theories, specifically in the context of computational theories, that is whose definition relies on rewriting. More specifically, combinations of computational theories will be studied in two contexts: ecumenical logics, i.e. logics that combine intuitionistic and classical logics, and theories of pure type systems modulo rewriting, which are used in the λΠ-calculus modulo theory to express logical systems of various proof assistants. First, we look at the special case of ecumenical logics, i.e. logics that combine intuitionistic and classical logics. A new ecumenical logic called NE is defined and studied. Its main properties are that its definition, though guided by, does not rely on double negations, and that it allows the definition of computational ecumenical theories, such as an ecumenical simple type theory. In a second time, the computational theories of pure type systems, an example of which is the logical framework of the λΠ-calculus modulo theory, are studied. In particular, we give tools to establish the well typedness of computational theories in a modular way, whether for extension or restriction (called fragmentation) of theories. Finally, we prove that for a given proof in a theory combining multiple fragments, it is possible to establish to which fragment this proof belongs from the constants it contains, without explicit indications of the rewriting rules used. This result is crucial in justifying the use of such theories for the interoperability of proof systems. Finally, based on the definition of NE and the previous modularity results, we focus on a computational theory of λΠ-calculus called theory U, combining first- and higher-order logics, minimal, intuitionistic, classical and ecumenical logics, prenex polymorphism and predicate subtyping, and the calculus of constructions. Properties of soundness, conservativity, consistency, normalization, and decidability of type-checking are established for the first- and higher-order logical fragments of theory U.
Members of the jury:
- Valeria de Paiva, Rapportrice & Examinatrice
- Cezary Kaliszyk, Rapporteur & Examinateur
- Elaine Pimentel, Examinatrice
- Jean-Baptiste Joinet, Examinateur
- Assia Mahboubi, Examinatrice
Formalised meta-theory for a certified type-theoretic kernel
Was on 17 December 2024.
Meven Lennon-Betrand (University of Cambrige)
Proof assistant kernels are a natural target for program certification: they are critical, yet small and well-specified. Still, despite the maturity of type theory and software verification, we are yet to see a certified Agda, Coq or Lean. In my talk, I will give an overview of the landscape around this grand goal, more particularly of the interaction between certification and meta-theory, and present two complementary formalisation projects in that direction.
The core difficulty is that kernels rely on complex invariants, which in turn rest on significant properties of the type system. In essence, we cannot certify a kernel without first formalising the meta-theory of its type system. Historically, emphasis has been put on the normalisation property. I will explain why, in my view, other properties are more important, in particular the one called injectivity of type constructors.
Strict Categories with Families
Was on 26 November 2024.
Loïc Pujet (University of Stockholm)

Categories with families (CwF) are perhaps the most widely used notion of models for dependent types. They can be described by an algebraic signature with dependent sorts for contexts, substitutions, types and terms, as well as a plethora of constants and equations. Unfortunately, this mix of dependent sorts and equations is particularly prone to transport hell, and in practice it is nearly impossible to prove non-trivial results using CwFs in a proof assistant.
In this talk, I will present a method based on Pédrot's "prefascist sets" to strictify (nearly) all the equations of a CwF, so that they hold by definition. I will then discuss applications of this method to formal proofs of canonicity and normalisation.
This is joint work with Ambrus Kaposi.
Towards a Type System for SMT-LIB v3
Was on 7 November 2024.
Ciarán Dunne (LMF)
The specification language SMT-LIB is the input language for SMT-solvers. Scripts in the SMT-LIB v2.6 represent configurations in many-sorted first-order logic (MFOL). A preliminary proposal for SMT-LIB v3 contemplates a significant shift from the traditional first-order setup to a higher-order logic with dependent types.
In this talk, we argue that the calculus of constructions (CC) is a suitable candidate for the abstract syntax of SMT-LIB v3. In particular, we demonstrate how concrete SMT instances, theories, and proofs can be interpreted in CC.
Moreover, we build on the work of Barras to give classical, set-theoretic semantics to our abstract syntax and make precise the central notion of satisfiability for SMT-LIB v3.
Finally, we will sketch out the details of how this interpretation can be leveraged to use Dedukti as a type-checker (and hence a proof-checker) for SMT-LIB v3.
Generation and automation of identity proofs in dependent type theory.
Was on 17 October 2024.
Thibaut Benjamin (University of Cambridge)
Dependent type theory based proof assistants are one of the tools offering the strongest guarantees on a software. However, in practical large scale project they induce a heavy proof effort, limiting their adoption. A common situation is that of a program using efficient datatypes, that lend themselves poorly to reasoning, making proofs very technical. A potential solution relies on the univalence principle proposed by Voevodski, stating that the correct notion of equality between datatypes is that of isomorphism. This allows one to transport programs and proofs on easy-to-reason-with but computationally inefficient datatypes to efficient ones. Unfortunately this principle is incompatible with that of uniqueness of identity proofs (UIP), another principle that is used to simplify reasoning. In practice, this means that reasoning under univalence requires one to carefully handle identity proofs, which is tricky. In this talk, I will present my work and a research direction allowing to simplify the handling of identity proofs. It relies on a tool I am developing called CaTT, allowing one to work in the algebraic structure of the identity types. I will show how the work in this tool can be partially automated, and I will demonstrate a Coq plug-in letting one generate computations on identity terms. This reduces the proof effort to manage identity types. Moreover, the incompatibility between the two principles entails that it is not sound to simultaneously use results from a library requiring univalence and from one requiring UIP. In practice though, some uses of UIP are superfluous, and it is sometimes possible to make the two library compatibles. The work I will present gives a hint towards a way to understand exactly when this is possible, and the degree of human intervention needed to do it.
The Max-Atom Problem applied to Universe Polymorphism in Type Theory
Was on 19 September 2024.
Marc Bezem (Universitetet i Bergen)
We give a short introduction to the Max-Atom Problem and its connection to type theory. Then we generalize to join-semilattices with an inflationary endomorphism and we explain how this generalization can be reformulated with Horn clauses (using an idea of Lorenzen). The key problems connected to universe polymorphism in type theory can now be formulated as loop checking problems and uniform word problems for this kind of lattices. Both can be solved by the computation of least Herbrand models of the corresponding Horn clauses.
In the second half of the talk we propose a type theory with explicit universe polymorphism, featuring level-indexed product types and constraint-indexed product types. In this type theory, loop checking and uniform word problems in the above mentioned lattices play a crucial role.
Efficiency and complexity issues will briefly be addressed throughout the talk. The research presented here is joint work with many people: Nieuwenhuis, Rodríguez-Carbonell, Coquand, Dybjer, Escardó.
PhD Defence: Generic Bidirectional Typing in a Logical Framework for Dependent Type Theories
Was on 18 September 2024.
Thiago will defend his PhD thesis.
The current version of the manuscript can be found here.
Abstract
Dependent type theories are formal systems that can be used both as programming languages and for the formalization of mathematics, and constitute the foundation of popular proof assistants such as Coq and Agda. In order to unify their study, Logical Frameworks (LFs) provide a unified meta-language for defining such theories in which various universal notions are built in by default and metatheorems can be proven in a theory-independent way.
This thesis focuses on LFs designed with implementation in mind, with the goal of providing generic type-checkers. Our main contribution is a new such LF which allows for representing type theories with their usual non-annotated syntaxes. The key to allowing the removal of annotations without jeopardizing decidability of typing is the integration of bidirectional typing, a discipline in which the typing judgment is decomposed into inference and checking modes. While bidirectional typing has been well known in the literature for quite some time, one of the central contributions of our work is that, by formulating it in an LF, we give it a generic treatment for all theories fitting our framework. Our proposal has been implemented in the generic type-checker BiTTs, allowing it to be used in practice with various theories.
In addition to our main contribution, we also advance the study of Dedukti, a sibling LF of our proposed framework. First, we revisit the problem of showing that theories are correctly represented in Dedukti by proposing a methodology for encodings which allows for showing their conservativity easily. Furthermore, we demonstrate how Dedukti can be used in practice as a tool for translating proofs by proposing a transformation for sharing proofs with predicative systems. This transformation has allowed for the translation of proofs from Matita to Agda, yielding the first-ever Agda proofs of Fermat's Little Theorem and Bertrand's Postulate.
Members of the jury:
- Andrej Bauer, University of Ljubljana - Reviewer
- Herman Geuvers, Radboud University Nijmegen - Reviewer
- Marc Bezem, University of Bergen
- Christine Paulin-Mohring, Université Paris-Saclay
- Temur Kutsia, Johannes Kepler University Linz
- Frank Pfenning, Carnegie Mellon University
- Frédéric Blanqui, Inria Saclay - Supervisor
- Gilles Dowek, Inria Saclay & ENS Paris-Saclay - Supervisor
Deducteam Intern Day
Was on 11 July 2024.
Interns (Deducteam)
The interns of our team will each give a talk about their respective ongoing internship.
This day will be preceded by Geoff Sutcliffe's talk at 9:30.
| Time | Talk |
|---|---|
| 9:30-10:30 | Geoff Sutcliffe — Proofs and Models in the TPTP World |
| 10:45-11:30 | Amal Maki — Translating Real Numbers from HOL-Light to Coq |
| 11:30-12:15 | Thomas Laure — Modelling of an intensional and extensional dependent types theory through sequential algorithms |
| 12:15-13:30 | Lunch in the ENS garden, bring and share |
| 13:45-14:30 | Salwa Tabet Gonzalez — Alignment of concepts: some experiments in Coq and LambdaPi |
| 14:30-15:15 | Ewen Broudin--Caradec — Toward subject reduction of Ghost Type Theory |
| 15:15-15:35 | Tomaz Mascarenhas — Proving Lean theorems via reconstructed SMT proofs |
Proofs and Models in the TPTP World
Was on 11 July 2024.
Geoff Sutcliffe (University of Miami)
This talk describes the representation of proofs and models in the TPTP World. Topics covered include the TPTP World, the TPTP language, the SZS ontologies, the representation of proofs and models, tools for visualizing and verifying proofs and models, and current work using Dedukti to verify derivations.
PhD Defence: Prétraitement compositionnel en Coq
Was on 10 July 2024.
Louise Dubois de Prisque (LMF)
Louise will defend her PhD thesis, in French.
Le manuscrit, en français également, est sur ma page web : https://louiseddp.github.io/.
Cette thèse présente une nouvelle méthodologie de prétraitement de buts de l'assistant de preuve Coq afin de les envoyer à un prouveur automatique.
Cette méthodologie consiste à composer des transformations atomiques et certifiantes en fonction du but à prouver.
Nous présenterons d'abord la bibliothèque de transformations que nous avons écrite,
puis nous présenterons un outil d'ordonnancement pour ces transformations, qui se veut générique.
Le tout a conduit à l'implémentation une nouvelle tactique 'pousse-bouton' appelée snipe pour Coq.
Jury :
- Sylvain Boulmé, Rapporteur & Examinateur, Maître de Conférences, Université Grenoble-Alpes
- Nicolas Tabareau, Rapporteur & Examinateur, Directeur de Recherche, INRIA
- Sylvie Boldo, Examinatrice, Directrice de Recherche, INRIA
- Sophie Tourret, Examinatrice, Chargée de Recherche, INRIA
- Yannick Forster, Invité, Chargé de Recherche, INRIA
Generalized Set Theories in Higher-Order Logic
Was on 6 June 2024.
Ciarán Dunne (LMF)
Set theories like Zermelo-Fraenkel (ZF) and Tarski-Grothendieck (TG) are "foundations of mathematics"; they provide a formal conception of set that is powerful and flexible enough for encoding a plethora of mathematical objects. When a set theory is used as the logical foundation of a proof assistant, nearly all mathematical objects have the same type, namely the type set. In contrast, many widely used proof assistants rely crucially on approaches where mathematical objects are organised into a vast number of types.
A generalized set theory (GST) is similar to a standard set theory, but allows having mathematical objects like pairs, functions, ordinals, etc., as objects that are not sets. Within a GST, all objects have the same (syntactic) type, but are partitioned into many soft types, which simulate some of the benefits of type theory.
In this talk, we explore the axiomatization and model construction techniques for GSTs in higher-order logic, and the implementation of both of these aspects in Isabelle/HOL.
Deductive systems and Grothendieck topologies
Was on 3 May 2024.
Olivia Caramello (University of Insubria, Como)
I will show that the classical proof system of geometric logic over a given geometric theory is equivalent to new proof systems based on the notion of Grothendieck topology. These equivalences result from a proof-theoretic interpretation of the duality between the quotients of a geometric theory and the subtoposes of its classifying topos. Interestingly, these new proof systems turn out to be computationally better-behaved than the classical one for many purposes, as I will illustrate by discussing a few selected applications.
Trocq: Proof Transfer for Free, With or Without Univalence
Was on 12 January 2024.
Enzo Crance (Gallinette, Inria Rennes, LS2N, Mitsubishi Electric)
Formalisation projects make use of a possibly broad range of different representations for a same mathematical concept. Yet, substantial manual input often remains necessary to switch from a representation to another, even though it is typically left implicit on paper. In this talk, we will present Trocq, a new proof transfer framework for dependent type theory. It is based on a generalisation of univalent parametricity, able to avoid dependency on the univalence axiom when possible, and able to exploit more relations that just equivalences. We will also present the implementation of Trocq, a plugin for the Coq proof assistant, written using the Coq-Elpi meta-language.
Fixed Point Theorems for Non-Transitive Relations
Was on 10 January 2024.
Jérémy Dubut-Kross (AIST, Tokyo)
We develop an Isabelle/HOL library of order-theoretic fixed-point theorems. We keep our formalization as general as possible: we reprove several well-known results about complete orders, often with only antisymmetry or attractivity, a mild condition implied by either antisymmetry or transitivity. In particular, we generalize various theorems ensuring the existence of a quasi-fixed point of monotone maps over complete relations, and show that the set of (quasi-)fixed points is itself complete. This result generalizes and strengthens theorems of Knaster-Tarski, Bourbaki-Witt, Kleene, Markowsky, Pataraia, Mashburn, Bhatta-George, and Stouti-Maaden.
Joint work with Akihisa Yamada.